|
|||||
|
|
|||||
INTRODUCTION AND OVERVIEW |
|||||
|
Sound is a physical phenomenon that transfers energy from
one point to another. In this respect, it is similar to radiation. It
differs from radiation, however, in that sound can pass only through
matter and not through a vacuum as radiation can. This is because sound
waves are actually vibrations passing through a material. If there is no
material, nothing can vibrate and sound cannot exist.
One of the most
significant characteristics of sound is its frequency, which is the rate
at which the sound source and the material vibrate. The basic unit for
specifying frequency is the hertz, which is one vibration, or cycle, per
second. Pitch is a term commonly used as a synonym for frequency of sound.
The human ear cannot hear or respond to all sound frequencies. The range of frequencies that can be heard by a normal young adult is from approximately 20 Hz to 20,000 Hz (20 kHz). Ultrasound has a frequency above this range. Frequencies in the range of 2 MHz (million cycles per second) to 20 MHz are used in diagnostic ultrasound. Ultrasound is used as a diagnostic tool because it can be focused into small, well-defined beams that can probe the human body and interact with the tissue structures to form images.
The transducer is
the component of the ultrasound imaging equipment that is placed in direct
contact with the patient's body. It performs several functions as will be
described in detail later. It's first function is to produce the
ultrasound pulses when electrical pulses are applied to it. A short
time later, when echo pulses return to the body surface they are picked up
by the transducer and converted back into electrical pulses that are then
processed by the system and formed into an image.
When a beam of ultrasound
pulses is passed into a body, several things happen. Most of the
ultrasound energy is absorbed and the beam is attenuated. This is
undesirable and does not contribute to the formation of an image like in
x-ray imaging. Some of the pulses will be reflected by internal body
structures and send echoes back to the surface where they are collected by
the transducer and used to form the image. Therefore, the general
ultrasound image is a display of structures or reflecting surfaces in the
body that produce echoes as illustrated below.
The Basic Ultrasound Imaging Process
Echoes, which
show up as bright or white spots in the image are produced by surfaces or
boundaries between two different types of tissues. Most anatomical
areas are composed of a "mixture" of different tissue types and many
surfaces that produce the general gray and white background that we see in
the image. Since there are no reflecting surfaces within a fluid,
such as a cyst, it is dark in the image. Therefore, the general
ultrasound image, sometimes called a "B mode" image, is a display of echo
producing sites within the anatomical area.
The ultrasound image is a display showing the
location of reflecting structures or echo sites within the body. The
location of a reflecting structure (interface) in the horizontal direction
is determined by the position of the beam. In the depth direction, it is
determined by the time required for the pulse to travel to the reflecting
site and for the echo pulse to return.
Another
physical characteristic that can be imaged with ultrasound is motion,
specifically the motion of flowing blood. This uses the Doppler
principle and the images are usually displayed with different colors
representing the different flow velocities and directions. This will
be covered in a later chapter.
|
|||||
THE ULTRASOUND IMAGING SYSTEM |
|||||
|
The basic functional components of an ultrasound imaging system are shown
below.
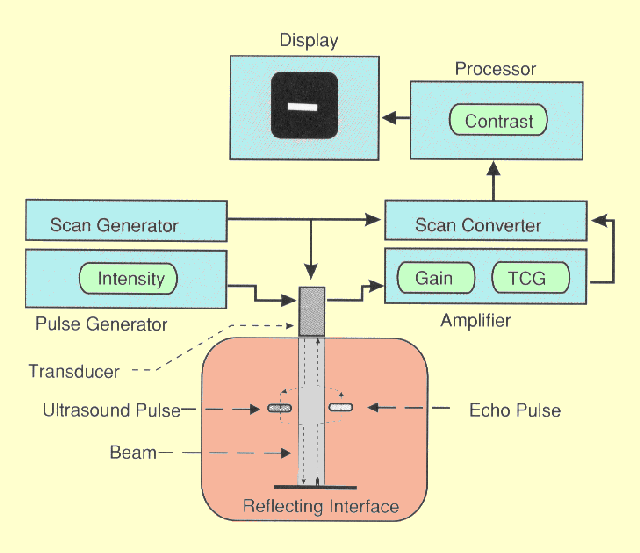 The Principal Functional Components of an Ultrasound Imaging System
Modern ultrasound systems use digital computer electronics to control most
of the functions in the imaging process. Therefore, the boxes in the
illustration above represent functions performed by the computer and other
electronic circuits and not individual physical components.
We will now
consider some of these functions in more detail and how they contribute to
image formation.
|
|||||
Transducer |
|
|
The transducer is the component of the ultrasound system
that is placed in direct contact with the patient's body. It alternates
between two major functions: (1) producing ultrasound pulses and (2)
receiving or detecting the returning echoes. Within the transducer there are one or
more piezoelectric elements. When an electrical pulse is applied to the
piezoelectric element it vibrates and produces the ultrasound. Also, when
the piezoelectric element is vibrated by the returning echo pulse it
produces a pulse of electricity.
The transducer also
focuses the beam of pulses to give it a specific size and shape at
various depths within the body and also scans the beam over the
anatomical area that is being imaged.
|
|
Pulse Generator |
|
|
The pulse generator produces the electrical pulses that are
applied to the transducer. For conventional ultrasound imaging the pulses
are produced at a rate of approximately 1,000 pulses per second. NOTE:
This is the pulse rate (pulses per second) and not the frequency
which is the number of cycles or vibrations per second within each pulse. The
principal control associated with the pulse generator is the size of the
electrical pulses that can be used to change the intensity and energy of the
ultrasound beam.
|
|
Amplification |
|
|
Amplification is used to increase the size of the electrical
pulses coming from the transducer after an echo is received.. The amount of amplification is
determined by the gain setting. The principal control associated with the
amplifier is the time gain compensation (TGC), which allows the user to
adjust the gain in relationship to the depth of echo sites within the
body. This function will be considered in much more detail in the next
section.
|
|
Scan Generator |
|
|
The scan generator controls the scanning of
the ultrasound beam over the body section being imaged. This is usually
done by controlling the sequence in which the electrical pulses are
applied to the piezoelectric elements within the transducer. This is also
considered in more detail later.
|
|
Scan Converter |
|
|
Scan conversion is the function that
converts from the format of the scanning ultrasound beam into a digital
image matrix format for processing and display.
|
|
Image Processor |
|
|
The digital image is processed to
produce the desired characteristics for display. This includes
giving it specific contrast characteristics and reformatting the image if
necessary.
|
|
Display |
|
|
The digital ultrasound images are viewed on the equipment display
(monitor) and usually transferred to the physician display or work
station.
One component
of the ultrasound imaging system that is not shown is the digital storage
device that is used to store images for later viewing if that process is
used.
|
|
|
|
|
THE ULTRASOUND PULSE |
|
The basic principles of ultrasound pulse production
and transmission are illustrated below.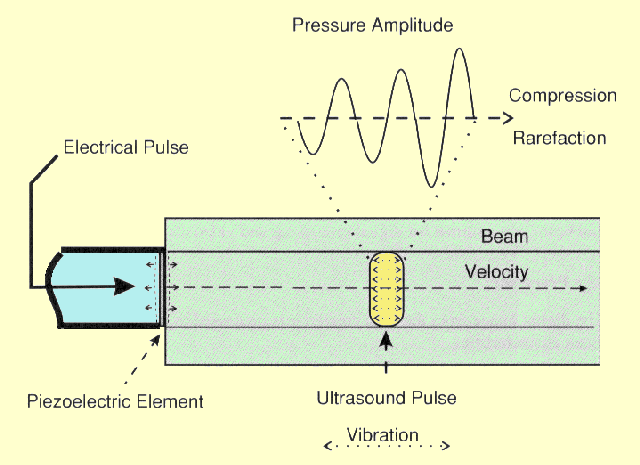
The Production of an Ultrasound Pulse
The source of sound is a vibrating object, the
piezoelectric transducer element. Since the vibrating source is in contact
with the tissue, it is caused to vibrate. The vibrations in the region of
tissue next to the transducer are passed on to the adjacent tissue. This
process continues, and the vibrations, or sound, is passed along from one
region of tissue to another. The rate at which the tissue structures
vibrate back and forth is the frequency of the sound. The rate at which
the vibrations move through the tissue is the velocity of the sound.
The sound in
most diagnostic ultrasound systems is emitted in pulses rather than a
continuous stream of vibrations. At any instant, the vibrations are
contained within a relatively small volume of the material. It is this
volume of vibrating material that is referred to as the ultrasound pulse.
As the vibrations are passed from one region of material to another, the
ultrasound pulse, but not the material, moves away from the source.
In soft tissue and fluid materials the direction of vibration is the same as the direction of pulse movement away from the transducer. This is characterized as longitudinal vibration as opposed to the transverse vibrations that occur in solid materials. As the longitudinal vibrations pass through a region of tissue, alternating changes in pressure are produced. During one half of the vibration cycle the tissue will be compressed with an increased pressure. During the other half of the cycle there is a reduction in pressure and a condition of rarefaction. Therefore, as an ultrasound pulse moves through tissue, each location is subjected to alternating compression and rarefaction pressures. As shown above, the space through which the ultrasound pulse moves is the beam. In a diagnostic system, pulses are emitted at a rate of approximately 1,000 per second. The pulse rate (pulses per second) should not be confused with the frequency, which is the rate of vibration of the tissue within the pulse and is in the range of 2-20 MHz. |
|
ULTRASOUND CHARACTERISTICS |
|
|
Ultrasound
pulses have several physical characteristics that should
be considered by the user in order to adjust the imaging procedure for specific
diagnostic applications. The most significant characteristics are
illustrated here.
|
|
|
The
Characteristics of Ultrasound Pulses That Have an Effect on the Imaging
Process
|
|
Frequency |
|
|
Ultrasound Pulse Frequency
The frequency of ultrasound pulses must
be carefully selected to provide a proper balance between image detail and
depth of penetration. In general, high frequency pulses produce higher
quality images but cannot penetrate very far into the body. These issues
will be discussed in greater detail later.
The frequency of sound is determined by the source. For example, in a piano, the source of sound is a string that is caused to vibrate by striking it. Each string within the piano is adjusted, or tuned, to vibrate with a specific resonant frequency. In diagnostic ultrasound equipment, the sound is generated by the transducer. The major element within the transducer is a crystal designed to vibrate with the desired frequency. A special property of the crystal material is that it is piezoelectric. This means that the crystal will deform if electricity is applied to it. Therefore, if an electrical pulse is applied to the crystal it will have essentially the same effect as the striking of a piano string: the crystal will vibrate. If the transducer is activated by a single electrical pulse, the transducer will vibrate, or "ring," for a short period of time. This creates an ultrasound pulse as opposed to a continuous ultrasound wave. The ultrasound pulse travels into the tissue in contact with the transducer and moves away from the transducer surface, as shown in the above figure. A given transducer is often designed to vibrate with only one frequency, called its resonant frequency. Therefore, the only way to change ultrasound frequency is to change transducers. This is a factor that must be considered when selecting a transducer for a specific clinical procedure. Certain frequencies are more appropriate for certain types of examinations than others. Some transducers are capable of producing different frequencies. For these the ultrasound frequency is determined by the electrical pulses applied to the transducer. |
|
Velocity |
|||||||||||
|
Factors Related to Ultrasound Pulse
Velocity
The significance of
ultrasound velocity is that it is used to determine the depth location of
structures in the body. The velocity with which sound travels through a
medium is determined by the characteristics of the material and not
characteristics of the sound. The velocity of longitudinal sound waves in
a liquid type medium like tissue is given by
___
where r is the density of the material, and
E is a
factor related to the elastic properties or "stiffness" of the material. The velocities
of sound through several materials of interest are given in the following
table.Velocity = ÖE/r
|
|||||||||||
|
|
|||||||||||
Wavelength |
|
|
The distance sound travels during the period of one vibration is
known as the wavelength,
l. Although wavelength is not a unique property
of a given ultrasound pulse, it is of some significance because it
determines the size (length) of the ultrasound pulse. This has an effect
on image quality, as we will see later.
The illustration below shows both temporal and spatial (length) characteristics related to the wavelength. A typical ultrasound pulse consists of several wavelengths or vibration cycles. The number of cycles within a pulse is determined by the damping characteristics of the transducer. Damping is what keeps the transducer element from continuing to vibrate and produce a long pulse. The wavelength is determined by the velocity, v, and frequency, f, in this relationship:
Wavelength
(l)
= v/f.
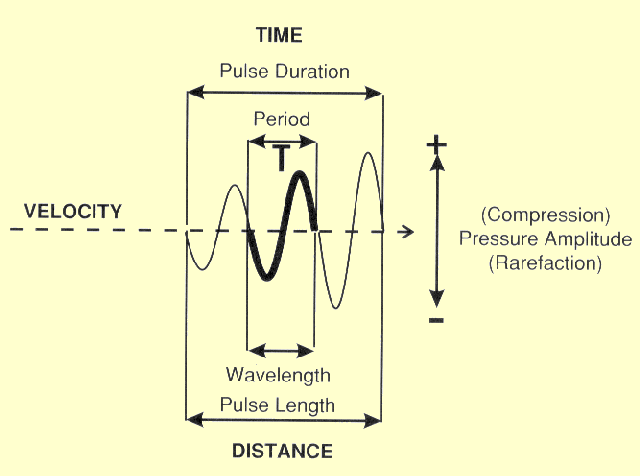
The Temporal and Length Characteristics of an Ultrasound Pulse
The period is the time required for one vibration cycle. It is the reciprocal of the frequency. Increasing the frequency decreases the period. In other words, wavelength is simply the ratio of velocity to frequency or the product of velocity and the period. This means that the wavelength of ultrasound is determined by the characteristics of both the transducer (frequency) and the material through which the sound is passing (velocity).
In ultrasound
imaging the significance of wavelength is that short wavelengths are
required to produce short pulses for good anatomical detail (in the depth
direction) and this requires higher frequencies as illustrated below.
Dependence of Pulse Length on Wavelength and Frequency
|
|
|
|
|
Amplitude |
|
|
The amplitude of an ultrasound pulse is the range of pressure excursions
as below.
Ultrasound Pulse Amplitude, Intensity, and Energy
. The pressure is related to the degree of tissue
displacement caused by the vibration. The amplitude is related to the
energy content, or "loudness," of the ultrasound pulse. The
amplitude of the pulse as it leaves the transducer is generally determined by how
hard the crystal is "struck" by the electrical pulse.
Most systems have a control on the pulse generator that changes the size
of the electrical pulse and the ultrasound pulse amplitude. We designate
this as the intensity control, although different names are used by
various equipment manufacturers.
In diagnostic applications, it is usually necessary to know only the
relative amplitude of ultrasound pulses. For example, it is necessary to
know how much the amplitude, A, of a pulse decreases as it passes through
a given thickness of tissue. The relative amplitude of two ultrasound
pulses, or of one pulse after it has undergone an amplitude change, can be
expressed by means of a ratio as follows:
Relative amplitude (ratio) = A2/A1.
There are advantages in expressing relative pulse amplitude in terms of
the logarithm of the amplitude ratio. When this is done the relative
amplitude is specified in units of decibels (dB). The relative pulse
amplitude, in decibels, is related to the actual amplitude ratio by
Relative amplitude (dB) = 20 log A2/A1
When the amplitude ratio is greater than 1 (comparing a large pulse to a
smaller one), the relative pulse amplitude has a positive decibel value;
when the ratio is less than 1, the decibel value is negative. In other
words, if the amplitude of a pulse is increased by some means, it will
gain decibels, and if it is reduced, it will lose decibels.
The following
illustration compares decibel values to pulse amplitude ratios and percent
values. The first two pulses differ in amplitude by 1 dB. In comparing the
second pulse to the first, this corresponds to an amplitude ratio of 0.89,
or a reduction of approximately 11%. If the pulse is reduced in amplitude
by another 11%, it will be 2 dB smaller than the original pulse. If the
pulse is once again reduced in amplitude by 11 % (of 79%), it will have an
amplitude ratio (with respect to the first pulse) of 0.71:1, or will be 3
dB smaller.
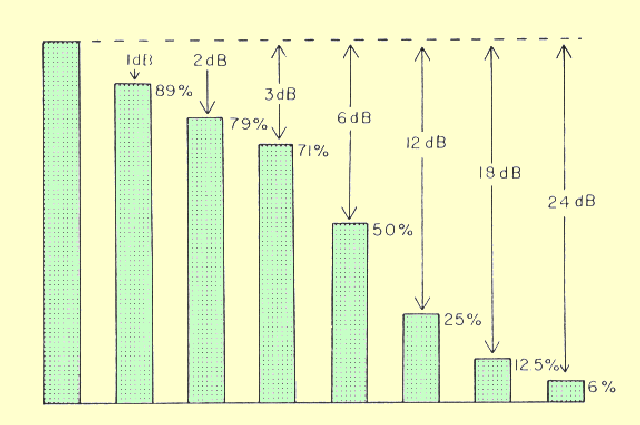
Pulse Amplitudes Expressed in Decibels and Percentages
Perhaps the best way to establish a "feel" for the relationship between pulse amplitude expressed in decibels and in percentage is to notice that amplitudes that differ by a factor of 2 differ by 6 dB. A reduction in amplitude of -6 dB divides the amplitude by a factor of 2, or 50%. The doubling of a pulse amplitude increases it by +6 dB.
During its lifetime, an ultrasound pulse undergoes many reductions in
amplitude as it passes through tissue because of absorption. If the amount
of each reduction is known in decibels, the total reduction can be found
by simply adding all of the decibel losses. This is much easier than
multiplying the various amplitude ratios.
|
|
INTENSITY AND POWER |
|
|
Power is the rate of energy transfer and is expressed in the units of
watts. Intensity is the rate at which power passes through a specified
area. It is the amount of power per unit area and is expressed in the
units of watts per square centimeter. Intensity is the rate at which
ultrasound energy is applied to a specific tissue location within the
patient's body. It is the quantity that must be considered with respect to
producing biological effects and safety. The intensity of most diagnostic
ultrasound beams at the transducer surface is on the order of a few
milliwatts per square centimeter.
Intensity is related to the pressure amplitude of the individual pulses
and the pulse rate. Since the pulse rate is fixed in most systems, the
intensity is determined by the pulse amplitude.
The relative intensity of two pulses (I1 and I2) can be expressed in the
units of decibels by:
Relative Intensity = 10 log I2/I1.
Note that when intensities are being considered, a factor of 10 appears in
the equation rather than a factor of 20, which is used for relative
amplitudes. This is because intensity is proportional to the square of the
pressure amplitude, which introduces a factor of 2 in the logarithmic
relationship. The intensity of an ultrasound beam is not constant with
respect to time nor uniform with respect to spatial area, as shown in the
following figure. This must be taken into consideration when describing
intensity. It must be determined if it is the peak intensity or the
average intensity that is being considered.
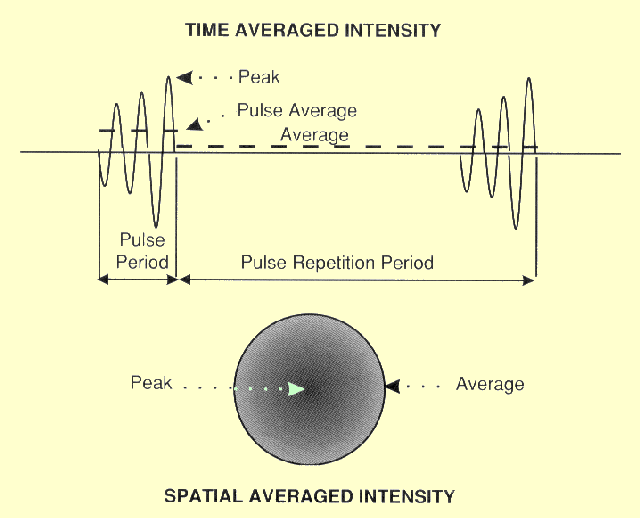
The Temporal and Spatial Characteristics of Ultrasound Pulses That Affect Intensity Values
|
|
Temporal Characteristics |
|
|
The figure
above shows two sequential pulses. Two important time intervals are
the pulse duration and the pulse repetition period. The ratio of the pulse
duration to the pulse repetition period is the duty factor. The duty
factor is the fraction of time that an ultrasound pulse is actually being
produced. If the ultrasound is produced as a continuous wave (CW), the
duty factor will have a value of 1. Intensity and power are proportional
to the duty factor. Duty factors are relatively small, less than 0.01, for
most pulsed imaging applications.
With respect to time there are three possible power (intensity) values.
One is the peak power, which is associated with the time of maximum
pressure. Another is the average power within a pulse. The lowest value is
the average power over the pulse repetition period for an extended time.
This is related to the duty factor.
|
|
Spatial Characteristics |
|
|
The energy or intensity is generally not distributed uniformly over the
area of an ultrasound pulse. It can be expressed either as the peak
intensity, which is often in the center of the pulse, for as the average
intensity over a designated area.
|
|
Temporal/Spatial Combinations |
|
|
There is some significance associated with each of the intensity
expressions. However, they are not all used to express the intensity with
respect to potential biological effects.
Thermal effects are most closely related to the spatial-peak and temporal-average intensity (ISPTA). This expresses the maximum intensity delivered to any tissue averaged over the duration of the exposure. Thermal effects (increase in temperature) also depend on the duration of the exposure to the ultrasound. Mechanical effects such as cavitation are more closely related to the spatial-peak, pulse-average intensity (ISPPA). |
|
INTERACTIONS OF ULTRASOUND WITH MATTER |
|
|
Three Types of Ultrasound Pulse
Interactions Within a Body
As an ultrasound pulse
passes through matter, such as human tissue, it interacts in several different ways. Some of these
interactions are necessary to form an ultrasound image, whereas others
absorb much of the ultrasound energy or produce artifacts and are
generally undesirable in diagnostic examinations. The ability to conduct
and interpret the results of an ultrasound examination depends on a
thorough understanding of these ultrasound interactions.
|
|
Absorption and Attenuation |
|||||||||||||||||
|
The Reduction of Pulse Amplitude by
Absorption of It's Energy
As the ultrasound pulse moves through matter, it continuously loses
energy. This is generally referred to as attenuation. Several factors
contribute to this reduction in energy. One of the most significant is the
absorption of the ultrasound energy by the material and its conversion
into heat. Ultrasound pulses lose energy continuously as they move through
matter. This is unlike x-ray photons, which lose energy in
"one-shot" photoelectric or Compton interactions. Scattering and
refraction interactions also remove some of the energy from the pulse and
contribute to its overall attenuation, but absorption is the most
significant.
The rate at which an ultrasound pulse is absorbed generally depends on two
factors: (1) the material through which it is passing, and (2) the
frequency of the ultrasound. The attenuation (absorption) rate is
specified in terms of an attenuation coefficient in the units of decibels
per centimeter. Since the attenuation in tissue increases with frequency,
it is necessary to specify the frequency when an attenuation rate is
given. The attenuation through a thickness of material, x, is given by:
Attenuation (dB) = (a) (f) (x)
where
a is the attenuation coefficient (in decibels per centimeter at 1
MHz), and f is the ultrasound frequency, in megahertz.
Approximate values
of the attenuation coefficient for various materials of interest are given
in the following table.
From the attenuation coefficient values given in
the above table, it is apparent
that there is a considerable variation in attenuation rate from material
to material. The significance of these values is now considered. Of all
the materials listed, water produces by far the least attenuation. This
means that water is a very good conductor of ultrasound. Water within the
body, such as in cysts and the bladder, forms "windows" through
which underlying structures can be easily imaged. Most of the soft tissues
of the body have attenuation coefficient values of approximately 1 dB per
cm per MHz, with the exception of fat and muscle. Muscle has a range of
values that depends on the direction of the ultrasound with respect to the
muscle fibers. Lung has a much higher attenuation rate than either air or
soft tissue. This is because the small pockets of air in the alveoli are
very effective in scattering ultrasound energy. Because of this, the
normal lung structure is extremely difficult to penetrate with ultrasound.
Compared to the soft tissues of the body, bone has a relatively high
attenuation rate. Bone, in effect, shields some parts of the body against
easy access by ultrasound.
The following
illustration shows the decrease in pulse amplitude as ultrasound passes
through various materials found in the human body.
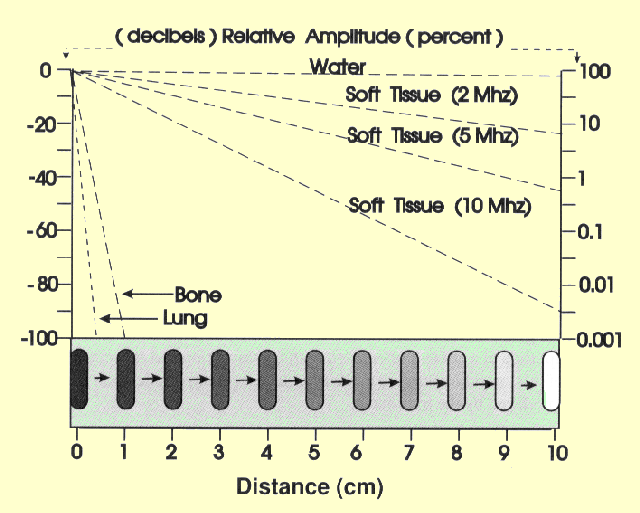
The Effect of Absorption on Ultrasound Pulse Amplitude in Relation to Distance or Depth in the Body
|
|||||||||||||||||
Reflection |
|||||||||||||||
|
The reflection of ultrasound pulses by structures within the body is the
interaction that creates the ultrasound image. The reflection of an
ultrasound pulse occurs at the interface, or boundary, between two
dissimilar materials, as shown in the following figure. In order to form a
reflection interface, the two materials must differ in terms of a physical
characteristic known as acoustic impedance Z. Although the traditional
symbol for impedance, Z, is the same symbol used for atomic number, the
two quantities are in no way related. Acoustic impedance is a
characteristic of a material related to its density and elastic
properties. Since the velocity is related to the same material
characteristics, a relationship exists between tissue impedance and
ultrasound velocity. The relationship is such that the impedance, Z, is
the product of the velocity, v, and the material density, Y, which can be
written as
Impedance = (Y) (v).
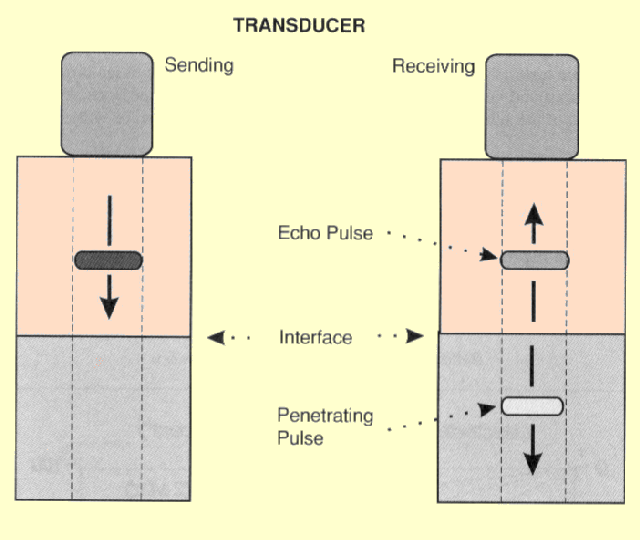
The Production of an Echo and Penetrating Pulse at a Tissue Interface
At most interfaces within the body, only a portion of the ultrasound pulse is reflected. The pulse is divided into two pulses, and one pulse, the echo, is reflected back toward the transducer and the other penetrates into the other material, as shown in the above figure. The brightness of a structure in an ultrasound image depends on the strength of the reflection, or echo. This in turn depends on how much the two materials differ in terms of acoustic impedance. The amplitude ratio of the reflected to the incident pulse is related to the tissue impedance values by
Reflection loss (dB) = 20 log (Z2 -
Z1)/(Z2 + Z1).
At most soft tissue interfaces, only a small fraction of the pulse is
reflected. Therefore, the reflection process produces relatively weak
echoes. At interfaces between soft tissue and materials such as bone,
stones, and gas, strong reflections are produced. The reduction in pulse
amplitude during reflection at several different interfaces is given in
the following table
The amplitude of a pulse is attenuated both by absorption and reflection losses. Because of this, an echo returning to the transducer is much smaller than the original pulse produced by the transducer. |
|||||||||||||||
Refraction |
|
|
When an ultrasound pulse passes through
an interface at a relatively small angle (between the beam direction and
interface surface), the penetrating pulse direction will be shifted by the
refraction process. This can produce certain artifacts as we will see
later..
|
|
PULSE DIAMETER AND BEAM WIDTH |
|
|
An important characteristic of an ultrasound pulse is its diameter, which
is also the width of the ultrasound beam. The diameter of a pulse changes
as it moves along the beam path. The effect of pulse size on image detail
will be considered in the next chapter.. At this point we will observe the change
in pulse diameter as it moves along the beam and show how it can be
controlled.
The diameter of the pulse is determined by the characteristics of the
transducer. At the transducer surface, the diameter of the pulse is the
same as the diameter of the vibrating crystal. As the pulse moves through
the body, the diameter generally changes. This is determined by the
focusing characteristics of the transducer.
|
|
Transducer Focusing |
|
|
Transducers can be designed to produce either a focused or non-focused
beam, as shown in the following figure. A focused beam is desirable for most
imaging applications because it produces pulses with a small diameter
which in turn gives better visibility of detail in the image. The best
detail will be obtained for structures within the focal zone. The distance
between the transducer and the focal zone is the focal depth.
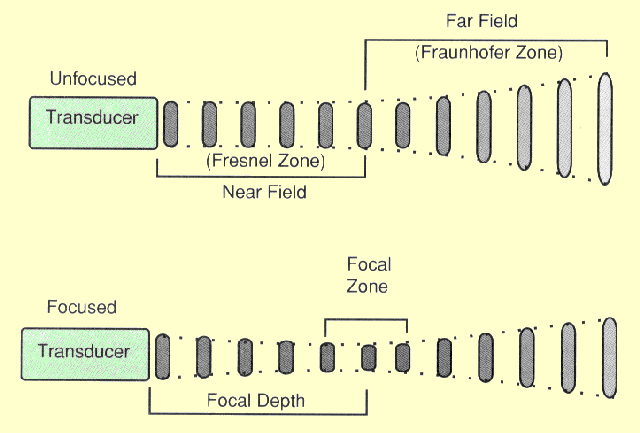
Beam Width and Pulse Diameter Characteristics of Both Unfocused and Focused Transducers
|
|
Unfocused Transducers |
|
|
An unfocused transducer produces a beam with two distinct regions, as
shown in the previous figure. One is the so-called near field or Fresnel zone and
the other is the far field or Fraunhofer zone.
In the near field, the ultrasound pulse maintains a relatively constant diameter that can be used for imaging.
In the near field, the beam has a constant diameter that is determined by
the diameter of the transducer. The length of the near field is related to
the diameter, D, of the transducer and the wavelength, l, of the
ultrasound by
Near field length = D2/4l.
Recall that the wavelength is inversely related to frequency. Therefore,
for a given transducer size, the length of the near field is proportional
to frequency. Another characteristic of the near field is that the
intensity along the beam axis is not constant; it oscillates between
maximum and zero several times between the transducer surface and the
boundary between the near and far field. This is because of the
interference patterns created by the sound waves from the transducer
surface. An intensity of zero at a point along the axis simply means that
the sound vibrations are concentrated around the periphery of the beam. A
picture of the ultrasound pulse in that region would look more like
concentric rings or "donuts" than the disk that has been shown
in various illustrations.
The major characteristic of the far field is that the beam diverges. This
causes the ultrasound pulses to be larger in diameter but to have less
intensity along the central axis. The approximate angle of divergence is
related to the diameter of the transducer, D, and the wavelength, l, by
Divergence angle (degrees) = 70l/D.
Because of the inverse relationship between wavelength and frequency,
divergence is decreased by increasing frequency. The major advantage of
using the higher ultrasound frequencies (shorter wavelengths) is that the
beams are less divergent and generally produce less blur and better
detail.
The previous
figure is a representation of the ideal ultrasound beam. However,
some transducers produce beams with side lobes. These secondary beams fan
out around the primary beam. The principal concern is that under some
conditions echoes will be produced by the side lobes and produce artifacts
in the image.
|
|
Fixed Focus |
|
|
A transducer can be designed to produce a focused ultrasound
beam by using a concaved piezoelectric element or an acoustic lens in
front of the element. Transducers are designed with different degrees of
focusing. Relatively weak focusing produces a longer focal zone and
greater focal depth. A strongly focused transducer will have a shorter
focal zone and a shorter focal depth.
Fixed focus transducers have the obvious disadvantages of not being able
to produce the same image detail at all depths within the body.
|
|
Adjustable Transmit Focus |
|
|
The focusing of some transducers can be
adjusted to a specific depth for each transmitted pulse. This concept is
illustrated in the following figure. The transducer is made up of an array of
several piezoelectric elements rather than a single element as in the
fixed focus transducer. There are two basic array configurations: linear
and annular. In the linear array the elements are arranged in either a
straight or curved line. The annular array transducer consists of
concentric transducer elements as shown. Although these two designs have
different clinical applications, the focusing principles are similar.
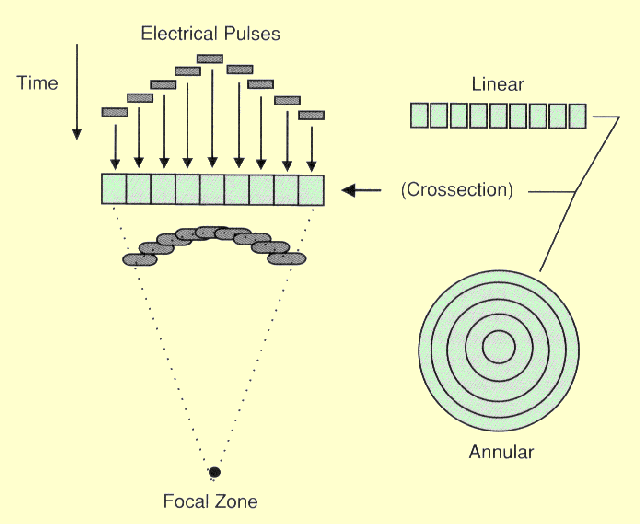
The Principle of Electronic Focusing with an Array Transducer
Focusing is achieved by not applying the electrical pulses to all of the
transducer elements simultaneously. The pulse to each element is passed
through an electronic delay. Now let's observe the sequence in which the
transducer elements are pulsed in the figure above. The outermost element
(annular) or elements (linear) will be pulsed first. This produces
ultrasound that begins to move away from the transducer. The other
elements are then pulsed in sequence, working toward the center of the
array. The centermost element will receive the last pulse. The pulses from
the individual elements combine in a constructive manner to create a
curved composite pulse, which will converge on a focal point at some
specific distance (depth) from the transducer.
The focal depth is determined by the time delay between the electrical
pulses. This can be changed electronically to focus pulses to give good
image detail at various depths within the body rather than just one depth
as with the fixed focus transducer. One approach is to create an image by
using a sequence of pulses, each one focused to a different depth or zone
within the body.
One distinction between the two transducer designs illustrated here is
that the annular array focuses the pulse in two dimensions whereas the
linear array can only focus in the one dimension; that is, in the plane of
the transducer.
|
|
Dynamic Receive Focus |
|
|
The focusing of an array transducer can also be
changed electronically when it is in the echo receiving mode. This is
achieved by processing the electrical pulses from the individual
transducer elements through different time delays before they are combined
to form a composite electrical pulse. The effect of this is to give the
transducer a high sensitivity for echoes coming from a specific depth
along the central axis of the beam. This produces a focusing effect for
the returning echoes.
An important factor is that the receiving focal depth can be changed
rapidly. Since echoes at different depths do not arrive at the transducer
at the same time, the focusing can be swept down through the depth range
to pick up the echoes as they occur. This is the major distinction between
dynamic or sweep focusing during the receive mode and adjustable transmit
focus. Any one transmitted pulse can only be focused to one specific
depth. However, during the receive mode, the focus can be swept through a
range of depths to pick up the multiple echoes produced by one transmit
pulse.
|
|
SUMMARY |
|
|
The ultrasound image is produced by
interactions of ultrasound pulses with the anatomical structures within
the human body. The basic B mode image is a display of echoes or
reflections from the structures and objects. The absorption of the
ultrasound as it passes into and back out of the body is generally
undesirable because it limits the depth of imaging, adversely affects the
amplitude of echoes that form the image, and can be the source of
artifacts.
The size of the
ultrasound pulse at different depths within the imaged area determines the
amount of blurring and image detail.
An understanding of
the physical characteristics of ultrasound and how it interacts with the
body enhances the ability to analyze images and make accurate diagnostic
decisions.
| |


No comments:
Post a Comment